Defining gyrotropic materials¶

Here we demonstrate the usage of Tidy3D simulation software for modeling of gyrotropic materials, that is, materials with Hermitian permittivity tensors. Currently, this is achieved by using fully anisotropic dieletric medium option with anisymmetric conductivity tensor. Specifically, let us consider modeling a material with total complex permittivity tensor $$\varepsilon = \varepsilon_u + i \frac{\sigma_u}{\omega} + i \varepsilon_0 G,$$ where $\varepsilon_u$ and $\sigma_u$ are real symmetric matrices describing unperturbed permittivity and conductivity of the material, and $G$ is a real antisymmetric matrix representing the magneto-optic effect. That is, $$G = \begin{pmatrix} 0 & g_z & -g_y \\ -g_z & 0 & g_x \\ g_y & -g_x & 0\end{pmatrix}$$ for a gyration vector $\boldsymbol{g} = \begin{pmatrix} g_x & g_y & g_z \end{pmatrix}$. Denoting the electromagnetic frequency of interest as $\omega_0$, we can approximate the complex permittivity of material in the vicinity of $\omega_0$ as $$\varepsilon \approx \varepsilon_u + i \frac{1}{\omega} \left( \sigma_u + \varepsilon_0 G \omega_0 \right).$$ Thus, the gyrotropic effect of a medium can be modeled by providing a modified conductivity tensor $\sigma = \sigma_u + \varepsilon_0 G \omega_0$ that contains both symmetric and antisymmetric parts. Note that because of this approximation, the simulation results will be most accurate in the vicinity of the frequency of interest $\omega_0$.

For more simulation examples, please visit our examples page. If you are new to the finite-difference time-domain (FDTD) method, we highly recommend going through our FDTD101 tutorials. FDTD simulations can diverge due to various reasons. If you run into any simulation divergence issues, please follow the steps outlined in our troubleshooting guide to resolve it.

Simulation setup¶

Let us now demonstrate simulation of plane wave propagation inside a gyrotropic material. Specifically, we will consider two simulations, one with $\boldsymbol{g} = 0$ and another one with $\boldsymbol{g} \neq 0$. In the first, reference, simulation the injected plane wave is expected to preserve its polarization, while in the second case the polarization of the injected pulse will undergo rotation due to the gyrotropic properties of the background medium. The rotation degree can be predicted by analytical expressions. In section Results we apply it to the results of the reference simulation and compare with the results of the gyrotropic simulation.

We define an elongated simulation domain assuming wave propagation along $z$ direction and select sample frequencies in the vicinity of the wavelength of interest.

Properties of the unperturbed material.

Gyration vector along the propagation axis.

Following the procedure outlined in the beginning of this tutorial we modify the material conductivity such that it accounts for material gyrotropic properties.

Now we define two materials: a simple isotropic medium to use in a reference simulation and a fully anisotropic medium for modeling the magneto-optic effect.

Given the simulation geometry we place PML boundary conditions along the propagation axis and periodic boundary conditions in the orthogonal directions

We will track field distribution along the propagation axis.

Since Tidy3D does not currently support injection of unidirectional plane waves into anisotropic material, we use a uniform current source to initiate a planar (bidirectional) propagating pulse.

Use automatic grid discretization based on the requested number of steps per source wavelength.

Combining defined above components we create two simulation, with and without gyrotropic effect.

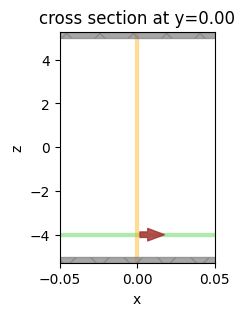
Visualize simulation for setup confirmation.

Results¶

Submit and run simulations on the server.

Now we compare the simulation results to analytically predicted behavior. It is known that in the gyrotropic medium propagation along gyration axis allows two circularly polarized normal modes with propagation constants given by $$n_{\pm} = \sqrt{n^2 \pm G}$$ and the rotatory power (rotation angle per unit length) of the medium is given by $$\rho = \frac{\pi}{\lambda_0} \left(n_- - n_+\right).$$

First we consider central frequency for which we expect simulation results to be the most accurate.

To obtain reference field distribution we extract numerical data from the reference simulation and apply rotation of polarization as predicted by the theory.

Extract simulation data at the chosen frequency.

Plot the comparison.

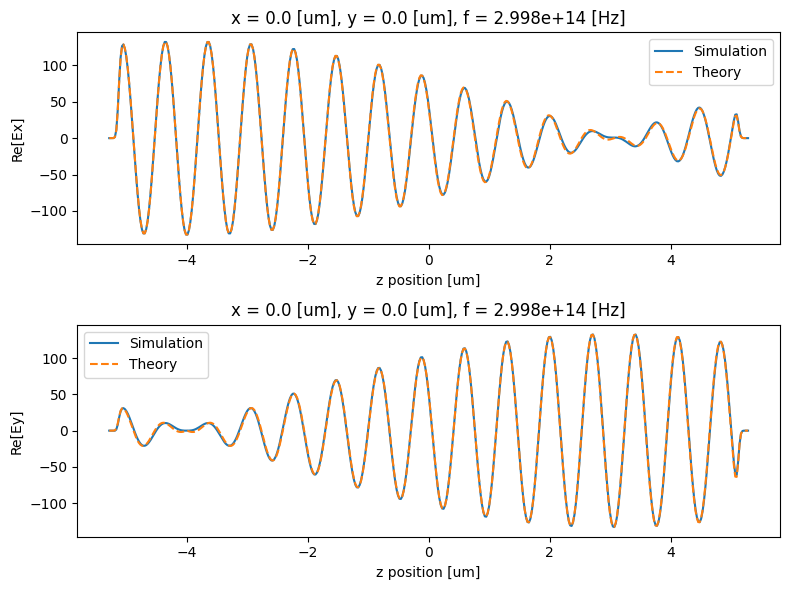
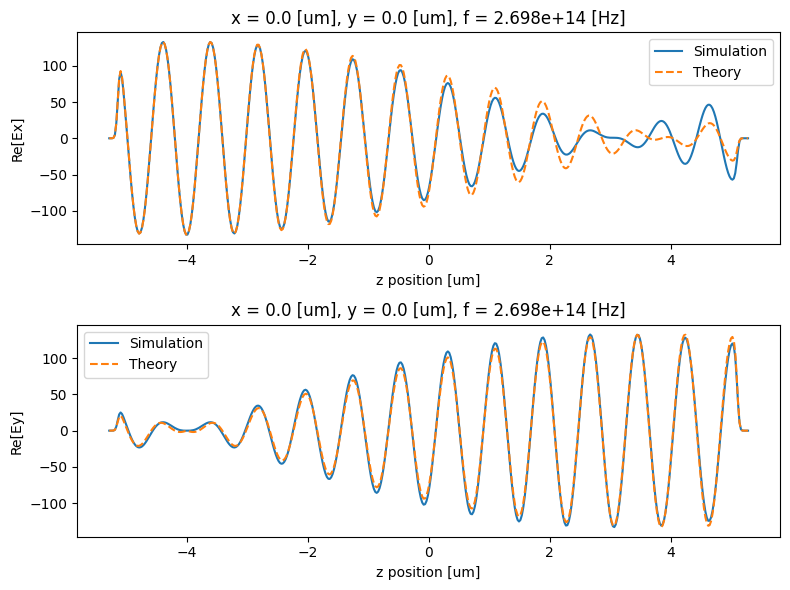
As one can see the simulation results for magneto-optic effect matches very closely the predicted behavior. Note that this comparison is made at the central wavelength. If we repeat the same comparison away from central wavelength the accuracy of simulation results will degrade because of the approximations made in defining properties of the gyrotropic medium.

Gyrotropic materials are only a special type of the FullyAnisotropicMedium. For more general cases, see the tutorial on defining fully anisotropic materials.