Learning Center

Inverse Design in Photonics An Introduction

By Tyler Hughes

“Inverse design” is a technique for automated photonic device design. The process involves mathematically defining a “figure of merit” for one’s device and then using gradient-based optimization to efficiently maximize this function with respect to a large number of design parameters. In this section, we introduce the basics of inverse design, discuss its connections to other techniques in deep learning, and give practical examples of how it is used to design photonic devices in Tidy3D.

Share On:

Download Tutorial: Notebook PDF

View Presentation Slides

Download Challenge: Notebook PDF

Additional information: This Session was updated in Mar 08, 2024

Previous Session

session_5_notebook

Inverse Design Workshop¶

This notebook will guide you through the basics of inverse design in Tidy3D using the adjoint plugin.

In [1]:

                                        import matplotlib
import matplotlib.pylab as plt
import numpy as np

import jax
import jax.numpy as jnp

import tidy3d as td
import tidy3d.plugins.adjoint as tda

                                      

We will be designing an integrated photonics device with 1 input port and 1 output port, connected by a rectangular "design" region.

This will be the starting point of our optimization work.

                      lx_des
                +--------------+    ^
                |              |    | ly_des
          ______|              |____|__
    --->             design         :    --->
    w_wg  ______     region     ____:__  w_wg
                |              |    |
                |              |    |
                +--------------+    V

Set up Simulation Base¶

Let's first define our global variables and design parameters.

In [2]:

                                        # spectral parameters
wavelength = 1.0
freq0 = td.C_0 / wavelength
fwidth = freq0 / 20
run_time = 100 / fwidth

# material parameters
eps_r_device = 2.75
eps_r_sub = 2.0

# geometric parameters
w_wg = 0.7 * wavelength
h_wg = 1.0 * wavelength
lx_des = 5.0 * wavelength
ly_des = 3.0 * wavelength
buffer_pml = 1.5 * wavelength
buffer_des = 1.5 * wavelength

# resolution parameters
min_steps_per_wvl = 20
pixel_size = 0.01

# monitor names
MNT_MODE = "mode"
MNT_FIELD = "field"

                                      

Quantities derived from above

In [3]:

                                        # total simulation size
Lx = buffer_pml + buffer_des + lx_des + buffer_des + buffer_pml
Ly = buffer_pml + ly_des + buffer_pml
Lz = 0.0

# source and monitor locations
x0_src = -Lx/2 + buffer_pml
x0_mnt = -x0_src

# number of design pixels in x and y
nx = int(np.ceil(lx_des / pixel_size))
ny = int(np.ceil(ly_des / pixel_size))

                                      

Now we will set up our "base" simulation out of all of these parameters.

Note, we will add the mode source and mode monitor after doing the mode solver.

In [4]:

                                        waveguide = td.Structure(
    geometry=td.Box(
        center=(0,0,0),
        size=(td.inf, w_wg, h_wg),
    ),
    medium=td.Medium(permittivity=eps_r_device)
)

design_region_geo = td.Box(
    center=(0, 0, 0),
    size=(lx_des, ly_des, h_wg),
)

mnt_field = td.FieldMonitor(
    size=(td.inf, td.inf, 0),
    center=(0,0,0),
    freqs=[freq0],
    name=MNT_FIELD,
)

                                      

In [5]:

                                        sim_base = tda.JaxSimulation(
    size=(Lx, Ly, Lz),
    structures=[waveguide],
    monitors=[mnt_field],
    grid_spec=td.GridSpec.auto(wavelength=wavelength, min_steps_per_wvl=min_steps_per_wvl),
    boundary_spec=td.BoundarySpec.pml(x=True, y=True, z=False),
    run_time=run_time,
)

                                      

Let's plot the base simulation.

In [6]:

                                        f, ax1 = plt.subplots(1,1, tight_layout=True, figsize=(10, 4))
sim_base.plot(z=0, ax=ax1)

# add design region
rmin, rmax = np.array(design_region_geo.bounds)
xy = (rmin[0], rmin[1])
width = design_region_geo.size[0]
height = design_region_geo.size[1]
des_region = matplotlib.patches.Rectangle(xy, width, height, fill=False)
ax1.add_patch(des_region)

plt.show()

                                      

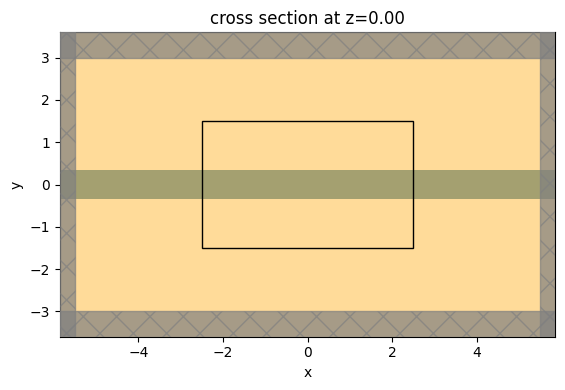
Categorize Waveguide Modes¶

Next we will use the mode solver to idenify which modes of interest exist in the simulation.

In [7]:

                                        from tidy3d.plugins.mode import ModeSolver

                                      

In [8]:

                                        plane_in = td.Box(
    size=(0, Ly, Lz or 1.0),
    center=(x0_src, 0, 0),
)

plane_out = td.Box(
    size=(0, Ly, Lz or 1.0),
    center=(x0_mnt, 0, 0),
)

num_modes = 4
mode_spec = td.ModeSpec(num_modes=num_modes)

                                      

In [9]:

                                        mode_solver = ModeSolver(
    simulation=sim_base.to_simulation()[0],
    plane=plane_in,
    mode_spec=mode_spec,
    freqs=[freq0],
)

                                      

In [10]:

                                        mode_data = mode_solver.solve()

                                      

11:11:54 EST WARNING: Use the remote mode solver with subpixel averaging for    
             better accuracy through 'tidy3d.plugins.mode.web.run(...)'.

In [11]:

                                        fig, axs = plt.subplots(num_modes, 3, figsize=(10, 3 * num_modes), tight_layout=True)
for mode_index in range(num_modes):
    vmax = 1.1 * max(abs(mode_data.field_components[n].sel(mode_index=mode_index)).max() for n in ("Ex", "Ey", "Ez"))
    for field_name, ax in zip(("Ex", "Ey", "Ez"), axs[mode_index]):
        field = mode_data.field_components[field_name].sel(mode_index=mode_index)
        field.real.plot(label="Real", ax=ax)
        field.imag.plot(ls="--", label="Imag", ax=ax)
        ax.set_title(f'index={mode_index}, {field_name}')
        ax.set_ylim(-vmax, vmax)
        ax.legend()

print(f"Effective index of computed modes: ", np.array(mode_data.n_eff))

                                      

Effective index of computed modes:  [[1.5724018 1.5359223 1.3050683 1.1859137]]

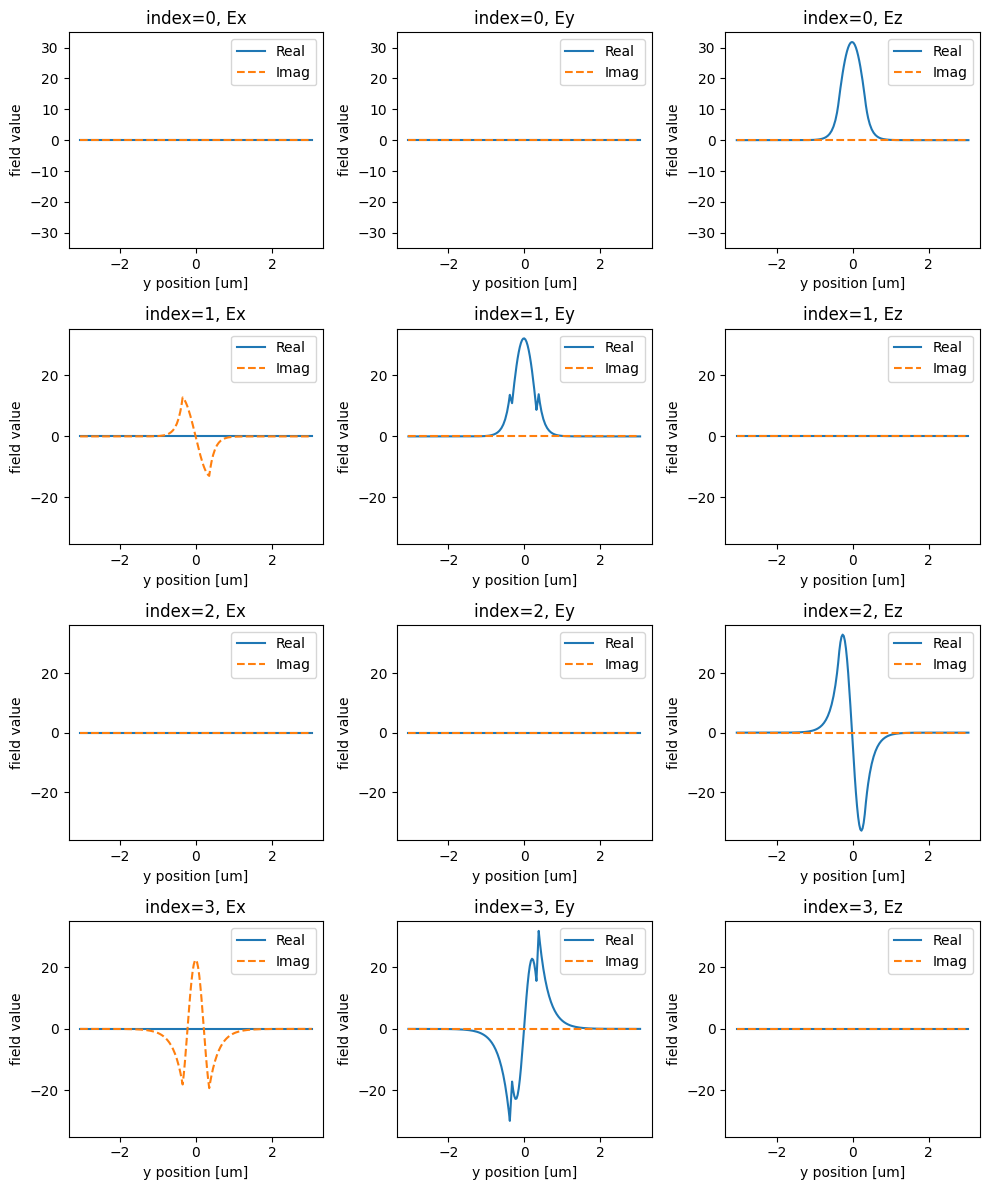
We note that the first and second order modes for the Ez polarization are indices 0 and 2, respectively, so we set some variables mode_index=0 for the source and mode_index=2 for the monitor.

In [12]:

                                        mode_index_in = 0
mode_index_out = 2

mode_index_max = max(mode_index_in, mode_index_out)
num_modes = mode_index_max + 1
mode_spec = td.ModeSpec(num_modes=num_modes)

                                      

Finally, we will use the mode solvers to export the source and monitor corresponding to our desired objective.

In [13]:

                                        src_mode = mode_solver.to_source(
    source_time=td.GaussianPulse(freq0=freq0, fwidth=fwidth),
    direction="+",
    mode_index=mode_index_in,
)

src_mode = src_mode.updated_copy(mode_spec=mode_spec)

                                      

In [14]:

                                        mnt_mode = mode_solver.to_monitor(
    name=MNT_MODE,
)

mnt_mode = mnt_mode.updated_copy(mode_spec=mode_spec, size=plane_out.size, center=plane_out.center)

Finally we add these to our base simulation.

In [15]:

                                        sim_base = sim_base.updated_copy(
    sources=[src_mode],
    output_monitors=[mnt_mode],
)

                                      

In [16]:

                                        f, ax1 = plt.subplots(1, 1, tight_layout=True, figsize=(10, 4))
sim_base.plot(z=0, ax=ax1)

# add design region
rmin, rmax = np.array(design_region_geo.bounds)
xy = (rmin[0], rmin[1])
width = design_region_geo.size[0]
height = design_region_geo.size[1]
des_region = matplotlib.patches.Rectangle(xy, width, height, fill=False)
ax1.add_patch(des_region)

plt.show()

                                      

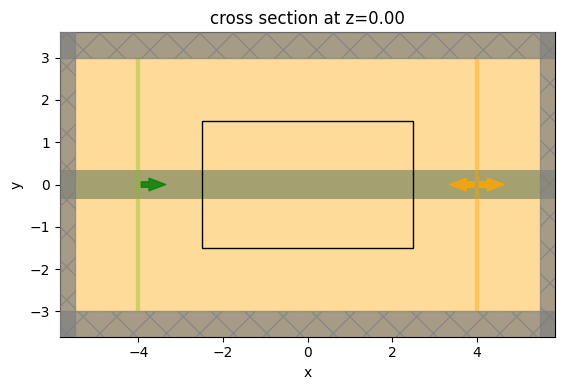
Define Design Parameters¶

Now we have a base simulation, but we need to define the design region as a function of the user-specified parameters.

We do this using python functions as this is the preferred method for jax.

In [17]:

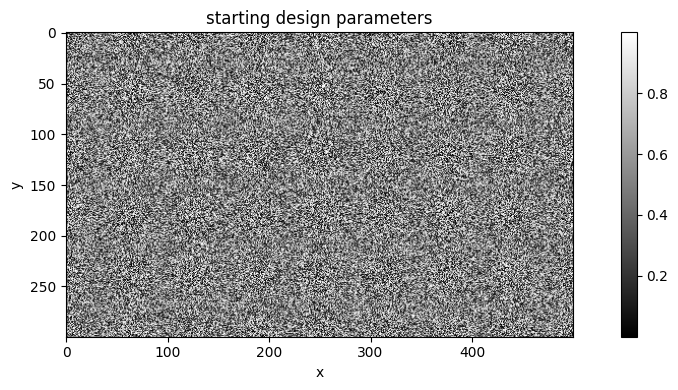
                                        # define some random parameters, uniform random between 0 and 1
params0 = np.random.uniform(size=(nx, ny))

In [18]:

                                        def plot_array(arr: np.ndarray, title: str="", ax=None, cmap="gray"):

    if ax is None:
        f, ax = plt.subplots(1, 1, tight_layout=True, figsize=(10, 4))
        ax = plt.gca()

    im = ax.imshow(arr.T, cmap=cmap)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_aspect('equal')
    ax.set_title(title)
    plt.colorbar(im, ax=ax)

                                      

In [19]:

                                        plot_array(params0, title="starting design parameters")

                                      

Feature size constraints¶

In [20]:

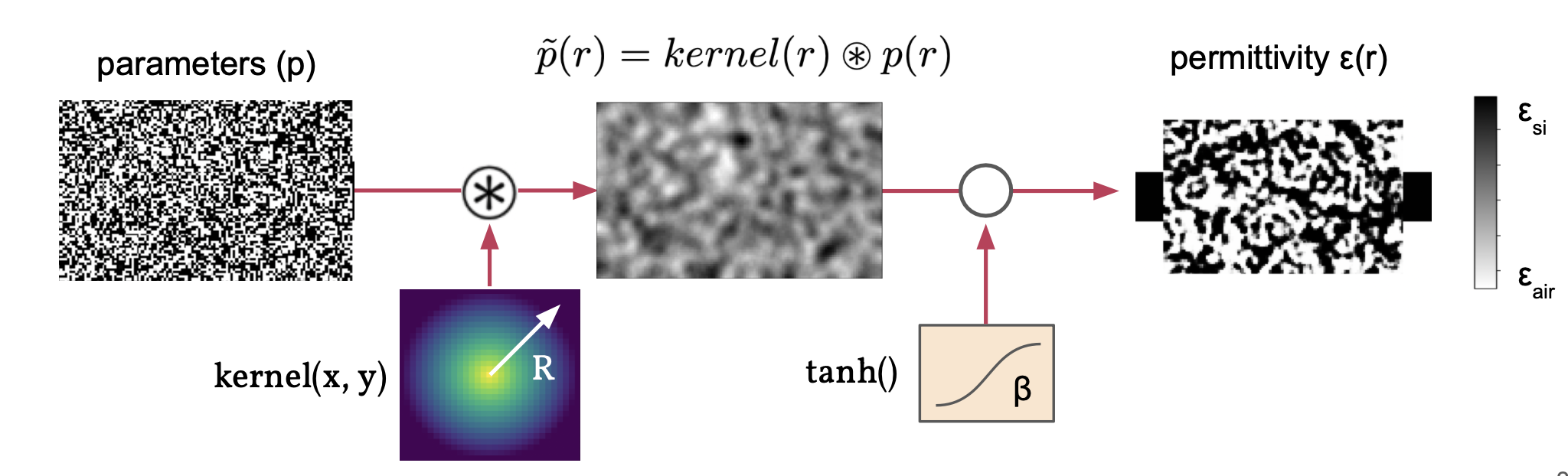
                                        from tidy3d.plugins.adjoint.utils.filter import ConicFilter, BinaryProjector

radius = 120e-3
beta_start = 1.0

conic_filter = ConicFilter(radius=radius, design_region_dl=pixel_size)

def material_density(params: jnp.ndarray, beta: float=beta_start, eta=0.5) -> jnp.ndarray:
    """Apply conic filter and binarization to the raw params."""
    params_smooth = conic_filter.evaluate(params)
    binary_projector = BinaryProjector(vmin=0, vmax=1, beta=beta, eta=eta)
    params_smooth_binarized = binary_projector.evaluate(params_smooth)
    return params_smooth_binarized

                                      

In [21]:

                                        def eps_values(params: np.ndarray, beta:float=beta_start) -> np.ndarray:
    """Compute the relative permittivity values from the user-defined parameters."""
    mat_density = material_density(params=params, beta=beta)
    return (1 - mat_density) + mat_density * eps_r_device

                                      

In [22]:

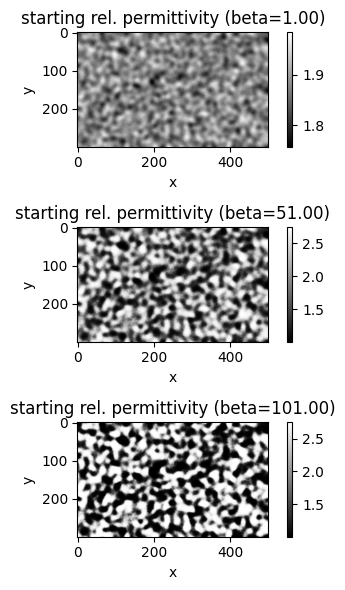
                                        num_betas = 3
betas = np.linspace(1, 101, num_betas)

f, axes = plt.subplots(num_betas, 1, tight_layout=True, figsize=(4, 2 * num_betas))

for beta, ax in zip(betas, axes):
    eps_test = eps_values(params0, beta=beta)
    plot_array(eps_test, title=f"starting rel. permittivity (beta={beta:.2f})", ax=ax)

                                      

In [23]:

                                        def get_structure(params: jnp.ndarray, beta: float=beta_start) -> tda.JaxStructureStaticGeometry:
    """Generate the structure used to define the design region."""

    values = eps_values(params=params, beta=beta).reshape((nx, ny, 1, 1))

    xs = np.linspace(-lx_des/2 + pixel_size/2, +lx_des/2 - pixel_size/2, nx).tolist()
    ys = np.linspace(-ly_des/2 + pixel_size/2, +ly_des/2 - pixel_size/2, ny).tolist()
    coords = dict(x=xs, y=ys, z=[0], f=[freq0])

    eps_data = tda.JaxDataArray(values=values, coords=coords)

    field_components = {f"eps_{dim}{dim}": eps_data for dim in "xyz"}
    eps_dataset = tda.JaxPermittivityDataset(**field_components)
    custom_medium = tda.JaxCustomMedium(eps_dataset=eps_dataset)
    custom_structure = tda.JaxStructureStaticGeometry(geometry=design_region_geo, medium=custom_medium)
    return custom_structure

                                      

In [24]:

                                        def get_simulation(params: jnp.ndarray, beta: float=beta_start) -> tda.JaxSimulation:
    """Generate the jax simulation as a funciton of the design parameters."""

    # mesh override structure (to get even meshing on the design region)
    design_region = get_structure(params=params, beta=beta)
    design_region_mesh = td.MeshOverrideStructure(
        geometry=design_region.geometry,
        dl=[pixel_size] * 3,
        enforce=True,
    )

    grid_spec = sim_base.grid_spec.updated_copy(override_structures=[design_region_mesh])

    jax_sim = sim_base.updated_copy(
        input_structures=[design_region],
        grid_spec=grid_spec,
    )

    return jax_sim

                                      

In [25]:

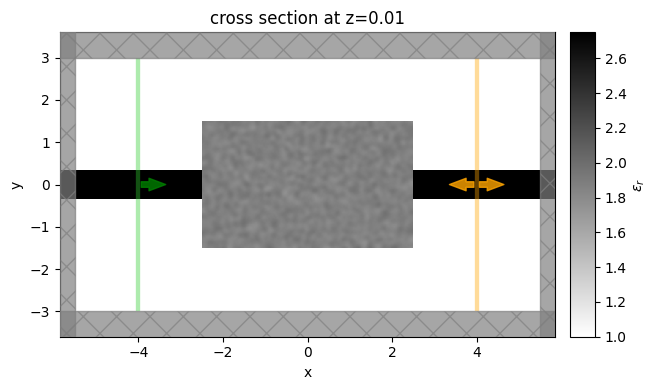
                                        sim0 = get_simulation(params0)

                                      

In [26]:

                                        f, ax1 = plt.subplots(1, 1, tight_layout=True, figsize=(10, 4))
sim0.plot_eps(z=0.01, ax=ax1)
plt.show()

                                      

Define Objective Function¶

In [27]:

                                        def get_coupling_efficiency(sim_data: tda.JaxSimulationData) -> float:
    """Return the coupling efficiecy between our desired input and output modes."""

    mnt_data = sim_data[MNT_MODE]
    amps = mnt_data.amps.sel(mode_index=mode_index_out, direction="+")
    amp = jnp.squeeze(amps.values)
    return jnp.abs(amp)**2

                                      

In [28]:

                                        from tidy3d.plugins.adjoint.utils.penalty import ErosionDilationPenalty

ed_penalty = ErosionDilationPenalty(length_scale=radius, pixel_size=pixel_size)

def penalty_fn(params: jnp.ndarray, beta: float=beta_start) -> float:
    """Compute penalty based on changes to structure under erosion and dilation."""
    mat_density = material_density(params=params, beta=beta)
    return ed_penalty.evaluate(mat_density)

                                      

In [29]:

                                        def objective(params: jnp.ndarray, beta: float=beta_start, verbose: bool=True, step_num: int=0) -> float:
    """Full objective function, incorporating coupling efficiency and feature size penalty."""

    # run simulation to compute coupling efficiency
    sim = get_simulation(params=params, beta=beta)
    sim_data = tda.web.run(sim, task_name="workshop", verbose=verbose)
    efficiency = get_coupling_efficiency(sim_data)

    # compute penalty and the weight based on beta
    penalty_val = penalty_fn(params=params, beta=beta)
    penalty_weight = np.minimum(1, beta/25)

    # compute full objective and dictionary of auxilary data
    objective_value = efficiency - penalty_weight * penalty_val
    aux_data = dict(efficiency=efficiency, penalty=penalty_val, objective=objective_value)

    return objective_value, aux_data

                                      

In [30]:

                                        val_grad_fn = jax.value_and_grad(objective, has_aux=True)

                                      

In [31]:

                                        (val, aux_data), grad = val_grad_fn(params0)

                                      

↓ jax_sim_vjp.hdf5 ━━━━━━━━━━━━━━━━━━━ 100.0% • 3.6/3.6 MB • 11.2 MB/s • 0:00:00

In [32]:

                                        print(val)

                                      

-0.039987057

In [33]:

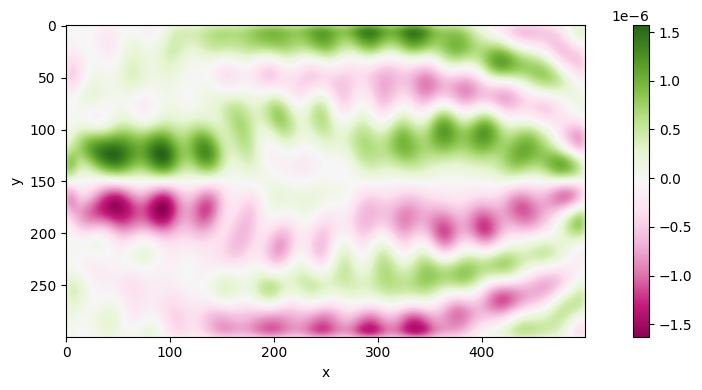
                                        print(grad)

                                      

[[-1.7771470e-08 -2.0668187e-08 -2.3562636e-08 ...  1.5108920e-08
   1.2763597e-08  1.0576878e-08]
 [-1.8935451e-08 -2.2087704e-08 -2.5253392e-08 ...  1.5637371e-08
   1.3093601e-08  1.0749200e-08]
 [-1.9465382e-08 -2.2783334e-08 -2.6150060e-08 ...  1.5460785e-08
   1.2785087e-08  1.0363090e-08]
 ...
 [ 1.9606199e-07  2.1697497e-07  2.3381583e-07 ... -2.4318797e-07
  -2.2439440e-07 -2.0176390e-07]
 [ 1.8335048e-07  2.0315522e-07  2.1916257e-07 ... -2.2792605e-07
  -2.1013133e-07 -1.8874621e-07]
 [ 1.6681594e-07  1.8497184e-07  1.9978364e-07 ... -2.0774851e-07
  -1.9134039e-07 -1.7176657e-07]]

In [34]:

                                        plot_array(grad, cmap="PiYG")

                                      

In [35]:

                                        import pprint
pprint.pprint(aux_data)

{'efficiency': Array(1.2938654e-05, dtype=float32),
 'objective': Array(-0.03998706, dtype=float32),
 'penalty': Array(0.99999994, dtype=float32)}

Optimize Device¶

In [36]:

                                        import optax

# hyperparameters
num_steps = 30
learning_rate = 0.5

# initialize adam optimizer with starting parameters
params = np.array(params0)
optimizer = optax.adam(learning_rate=learning_rate)
opt_state = optimizer.init(params)

# store history
history = dict(
    params=[],
    grad=[],
    objective=[],
    efficiency=[],
    penalty=[],
    beta=[],
)

# gradually increase the binarization strength
beta0 = beta_start
beta_increment = 1.0

for i in range(num_steps):
    print(f"step = ({i + 1} / {num_steps})")

    # compute gradient and current objective funciton value
    beta = beta0 + i * beta_increment
    (val, aux_data), grad = val_grad_fn(params, beta=beta, verbose=False, step_num=i)
    efficiency = aux_data["efficiency"]
    penalty = aux_data["penalty"]

    # outputs
    print(f"\tbeta = {beta:.2e}")
    print(f"\tobjective fn = {val:.2e}")
    print(f"\t\tefficiency = {efficiency:.2e}")
    print(f"\t\tpenalty    = {penalty:.2e}")
    print(f"\t|gradient| = {np.linalg.norm(grad):.2e}")

    # save history
    history["params"].append(params)
    history["grad"].append(grad)
    history["objective"].append(val)
    history["efficiency"].append(efficiency)
    history["penalty"].append(penalty)
    history["beta"].append(beta)

    # compute and apply updates to the optimizer based on gradient (-1 sign to maximize obj_fn)
    if i < num_steps - 1:
        updates, opt_state = optimizer.update(-grad, opt_state, params)
        params = optax.apply_updates(params, updates)

        # cap the parameters between (0, 1)
        params = jnp.minimum(params, 1.0)
        params = jnp.maximum(params, 0.0)

                                      

step = (1 / 30)
	beta = 1.00e+00
	objective fn = -4.00e-02
		efficiency = 1.29e-05
		penalty    = 1.00e+00
	|gradient| = 2.05e-04
step = (2 / 30)
	beta = 2.00e+00
	objective fn = 1.03e-01
		efficiency = 1.83e-01
		penalty    = 1.00e+00
	|gradient| = 1.96e-02
step = (3 / 30)
	beta = 3.00e+00
	objective fn = -5.31e-02
		efficiency = 3.72e-02
		penalty    = 7.53e-01
	|gradient| = 1.19e-02
step = (4 / 30)
	beta = 4.00e+00
	objective fn = -8.28e-02
		efficiency = 1.98e-02
		penalty    = 6.41e-01
	|gradient| = 6.84e-03
step = (5 / 30)
	beta = 5.00e+00
	objective fn = 7.71e-02
		efficiency = 1.70e-01
		penalty    = 4.63e-01
	|gradient| = 1.17e-02
step = (6 / 30)
	beta = 6.00e+00
	objective fn = 1.81e-01
		efficiency = 2.71e-01
		penalty    = 3.76e-01
	|gradient| = 1.96e-02
step = (7 / 30)
	beta = 7.00e+00
	objective fn = 3.99e-01
		efficiency = 4.84e-01
		penalty    = 3.03e-01
	|gradient| = 1.33e-02
step = (8 / 30)
	beta = 8.00e+00
	objective fn = 5.02e-01
		efficiency = 5.88e-01
		penalty    = 2.67e-01
	|gradient| = 1.43e-02
step = (9 / 30)
	beta = 9.00e+00
	objective fn = 5.74e-01
		efficiency = 6.64e-01
		penalty    = 2.50e-01
	|gradient| = 1.74e-02
step = (10 / 30)
	beta = 1.00e+01
	objective fn = 6.22e-01
		efficiency = 7.12e-01
		penalty    = 2.25e-01
	|gradient| = 1.47e-02
step = (11 / 30)
	beta = 1.10e+01
	objective fn = 6.85e-01
		efficiency = 7.76e-01
		penalty    = 2.06e-01
	|gradient| = 7.44e-03
step = (12 / 30)
	beta = 1.20e+01
	objective fn = 7.18e-01
		efficiency = 8.10e-01
		penalty    = 1.92e-01
	|gradient| = 1.21e-02
step = (13 / 30)
	beta = 1.30e+01
	objective fn = 7.42e-01
		efficiency = 8.33e-01
		penalty    = 1.76e-01
	|gradient| = 1.14e-02
step = (14 / 30)
	beta = 1.40e+01
	objective fn = 7.68e-01
		efficiency = 8.60e-01
		penalty    = 1.65e-01
	|gradient| = 6.65e-03
step = (15 / 30)
	beta = 1.50e+01
	objective fn = 7.88e-01
		efficiency = 8.81e-01
		penalty    = 1.54e-01
	|gradient| = 6.84e-03
step = (16 / 30)
	beta = 1.60e+01
	objective fn = 7.96e-01
		efficiency = 8.87e-01
		penalty    = 1.41e-01
	|gradient| = 1.22e-02
step = (17 / 30)
	beta = 1.70e+01
	objective fn = 8.10e-01
		efficiency = 8.99e-01
		penalty    = 1.31e-01
	|gradient| = 1.39e-02
step = (18 / 30)
	beta = 1.80e+01
	objective fn = 8.25e-01
		efficiency = 9.19e-01
		penalty    = 1.30e-01
	|gradient| = 9.50e-03
step = (19 / 30)
	beta = 1.90e+01
	objective fn = 8.39e-01
		efficiency = 9.34e-01
		penalty    = 1.26e-01
	|gradient| = 5.04e-03
step = (20 / 30)
	beta = 2.00e+01
	objective fn = 8.35e-01
		efficiency = 9.30e-01
		penalty    = 1.19e-01
	|gradient| = 1.03e-02
step = (21 / 30)
	beta = 2.10e+01
	objective fn = 8.40e-01
		efficiency = 9.38e-01
		penalty    = 1.17e-01
	|gradient| = 1.14e-02
step = (22 / 30)
	beta = 2.20e+01
	objective fn = 8.44e-01
		efficiency = 9.45e-01
		penalty    = 1.15e-01
	|gradient| = 9.66e-03
step = (23 / 30)
	beta = 2.30e+01
	objective fn = 8.49e-01
		efficiency = 9.50e-01
		penalty    = 1.10e-01
	|gradient| = 7.67e-03
step = (24 / 30)
	beta = 2.40e+01
	objective fn = 8.53e-01
		efficiency = 9.57e-01
		penalty    = 1.08e-01
	|gradient| = 3.84e-03
step = (25 / 30)
	beta = 2.50e+01
	objective fn = 8.53e-01
		efficiency = 9.58e-01
		penalty    = 1.05e-01
	|gradient| = 6.15e-03
step = (26 / 30)
	beta = 2.60e+01
	objective fn = 8.55e-01
		efficiency = 9.56e-01
		penalty    = 1.01e-01
	|gradient| = 1.01e-02
step = (27 / 30)
	beta = 2.70e+01
	objective fn = 8.59e-01
		efficiency = 9.59e-01
		penalty    = 9.98e-02
	|gradient| = 8.84e-03
step = (28 / 30)
	beta = 2.80e+01
	objective fn = 8.67e-01
		efficiency = 9.63e-01
		penalty    = 9.65e-02
	|gradient| = 4.86e-03
step = (29 / 30)
	beta = 2.90e+01
	objective fn = 8.69e-01
		efficiency = 9.61e-01
		penalty    = 9.16e-02
	|gradient| = 6.42e-03
step = (30 / 30)
	beta = 3.00e+01
	objective fn = 8.70e-01
		efficiency = 9.63e-01
		penalty    = 9.28e-02
	|gradient| = 6.81e-03

Analyze Results¶

In [37]:

                                        objectives = np.array(history["objective"])
efficiencies = np.array(history["efficiency"])
penalties = np.array(history["penalty"])

num_iters_completed = len(objectives)
iterations = np.arange(num_iters_completed)

                                      

In [38]:

                                        objective_start = objectives[0]
objective_final = objectives[-1]
objective_change = objective_final - objective_start

efficiency_start = efficiencies[0]
efficiency_final = efficiencies[-1]
efficiency_change = efficiency_final - efficiency_start

penalty_start = penalties[0]
penalty_final = penalties[-1]
penalty_change = penalty_final - penalty_start

print(f"After {num_iters_completed} iterations:")
print(f'\t-> objecitve function changed from : \t{objective_start:+.2f} -> {objective_final:+.2f} ({objective_change:+.2f})')
print(f'\t-> coupling efficiency changed from : \t{efficiency_start:+.2f} -> {efficiency_final:+.2f} ({efficiency_change:+.2f})')
print(f'\t-> fabrication penalty changed from : \t{penalty_start:+.2f} -> {penalty_final:+.2f} ({penalty_change:+.2f})')

                                      

After 30 iterations:
	-> objecitve function changed from : 	-0.04 -> +0.87 (+0.91)
	-> coupling efficiency changed from : 	+0.00 -> +0.96 (+0.96)
	-> fabrication penalty changed from : 	+1.00 -> +0.09 (-0.91)

In [39]:

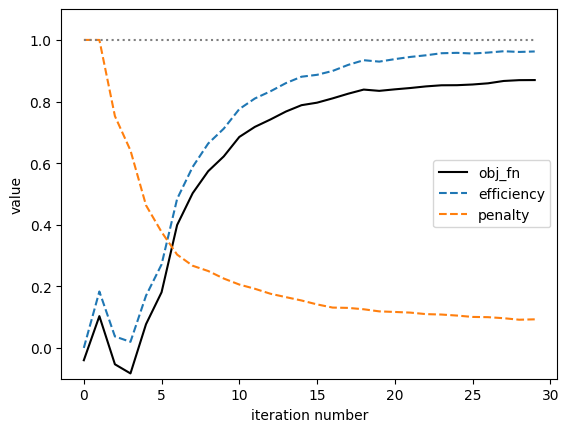
                                        plt.plot(iterations, objectives, label="obj_fn", color="k")
plt.plot(iterations, efficiencies, label="efficiency", linestyle="--")
plt.plot(iterations, penalties, label="penalty", linestyle="--")
plt.plot(iterations, np.ones_like(iterations), color="grey", linestyle=':')
plt.xlabel('iteration number')
plt.ylabel('value')

plt.ylim([-0.1, 1.1])
plt.legend()

plt.show()

                                      

In [40]:

                                        params_final = history["params"][-1]
beta_final = history["beta"][-1]
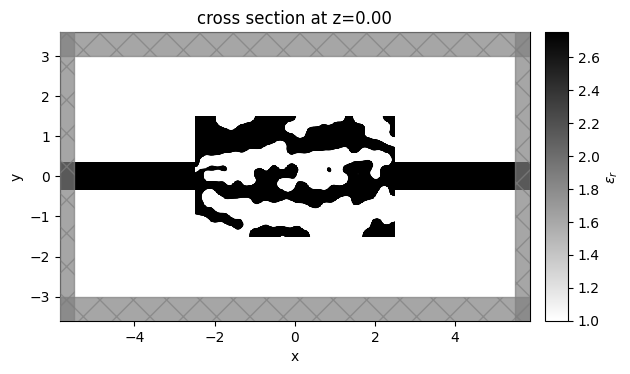
jax_sim_final = get_simulation(params=params_final, beta=beta_final)
sim_final = jax_sim_final.to_simulation()[0]

                                      

In [41]:

                                        ax = sim_final.plot_eps(z=0, monitor_alpha=0, source_alpha=0)

                                      

In [42]:

                                        sim_data_final = td.web.run(sim_final, task_name="invdes_final")

                                      

↓ simulation_data.hdf5.gz ━━━━━━━━━━━ 100.0% • 13.1/13.1   • 19.1 MB/s • 0:00:00
                                               MB

11:49:09 EST loading simulation from simulation_data.hdf5

In [43]:

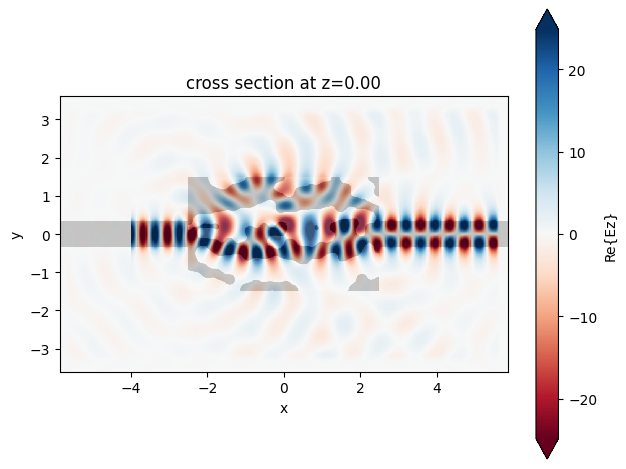
                                        ax = sim_data_final.plot_field(MNT_FIELD, field_name="Ez", val="real")

                                      

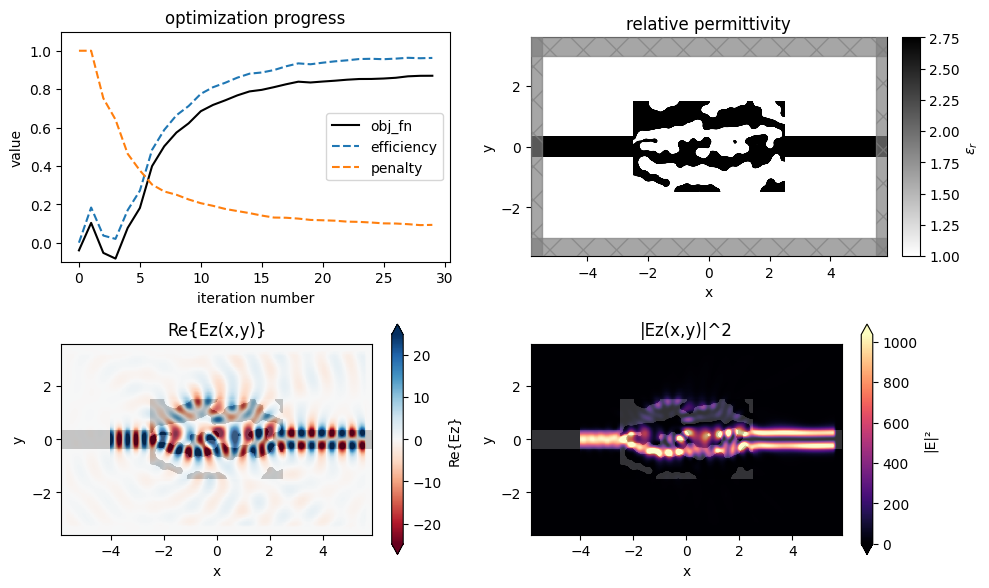
Finally let's make a nice figure combining all of the data.

In [44]:

                                        f, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, tight_layout=True, figsize=(10, 6))

ax1.plot(iterations, objectives, label="obj_fn", color="k")
ax1.plot(iterations, efficiencies, label="efficiency", linestyle="--")
ax1.plot(iterations, penalties, label="penalty", linestyle="--")
ax1.set_xlabel('iteration number')
ax1.set_ylabel('value')
ax1.set_ylim([-0.1, 1.1])
ax1.legend()
ax1.set_title('optimization progress')

ax2 = sim_final.plot_eps(z=0, monitor_alpha=0, source_alpha=0, ax=ax2)
ax2.set_title('relative permittivity')

ax3 = sim_data_final.plot_field(MNT_FIELD, field_name="Ez", val="real", ax=ax3)
ax3.set_title('Re{Ez(x,y)}')

ax4 = sim_data_final.plot_field(MNT_FIELD, field_name="E", val="abs^2", ax=ax4)
ax4.set_title('|Ez(x,y)|^2')

# plt.savefig('invdes.png') # uncomment to save
plt.show()

                                      

In [ ]:

Download Presentation